佛山铝单板厂家哪里有售（列空间行空间零空间）行空间的基和列空间的基，

3月11日更新：说明一下，这个回答和原问题是有出入的矩阵本身就是一个人为定义的概念，行空间和列空间则是对矩阵从不同方向拆分、从几何角度一种理解而行空间和列空间本身又不是绝对的对一个矩阵转置，行空间就变成列空间了；但实际上空间还是原来那两个空间，矩阵也还是原来那些个数组，换个名字、换个顺序罢了。

所以本来行空间和列空间是等价的概念，只是因为通常把向量乘在右边，所以在运算时表现出性质的差异如果习惯是乘在左边，两者性质就要掉个个行空间和列空间有没有关系，有（见原回答），当然这里的映射都是建立在“右乘

”的大前提之上两个空间能不能转换，我觉得这个问题意义不大，因为他们本身就是一个矩阵的两种不同表示，你大可以先还原成矩阵再换过去不过如果实在要问“两个空间能不能直接互相转换”，我只能说，不知道------------------------------------------------------------------------------------------------------------------------------。

（以下是原回答）其实矩阵就是一个将向量由行空间向列空间映射的运算。假设在A(m*n)的行空间中有任一向量x，Ax=b ，那么 b 在 A 的列空间中。

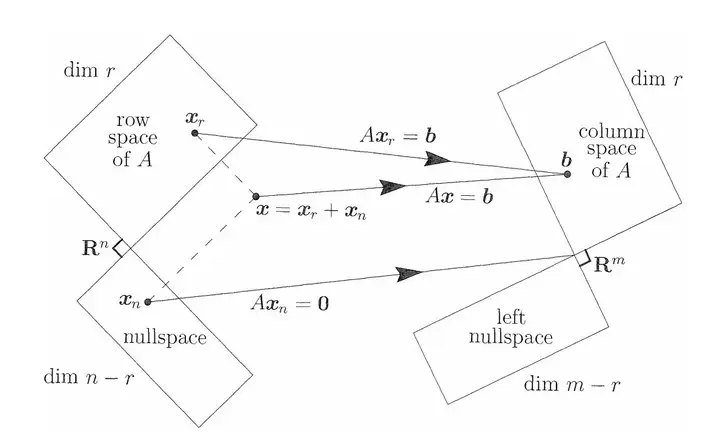
从维的角度也很好理解，x 是 n维的，b 就变成 m 维的了。反之亦然（下面这张双向的图）。

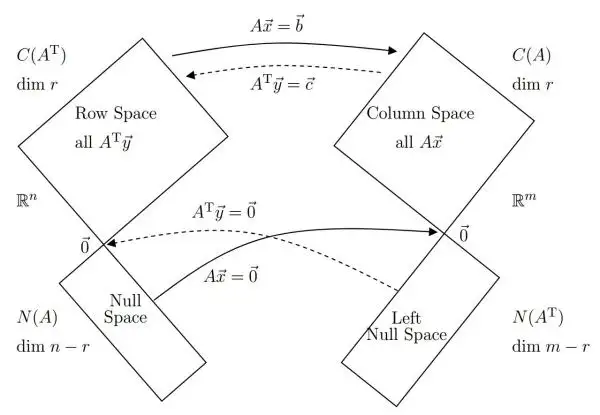
两张图片来自 Gilbert Strang - Linear Algebra and its applications (Fouth Edition).