浅谈教师课堂提问的艺术（教师课堂提问的技巧与策略）

——福建省宁德市教育局薛赞祥提问是小学数学课堂教学的重要手段，是启发学生思维的主要途径目前，小学数学课堂教学中“问而不发”、“问而乱发”的现象屡见不鲜，究其原因，主要是问不得法问是发的条件，发是问的结果，要求学生发得好，教师首先要问得好。

教师怎样才能问得好呢？关键要在因材（教材）设问方面做文章，也就是要根据教材内容设计“问什么”；同时要在因才（学生）施问方面下功夫，也就是要根据学生实际设计“怎么问”因材设问一.问起点起点，即认知的固定点，是指学生原有认知结构中对新知的学习起稳固作用的观念，是生长新知的基础，是“拴住”新知的“锚桩”。

为此，教师要把新知识放在整个旧知识的背景中去考虑，从旧知识中准确地找到新知识的认知生长点，设计出导向式的问题，为学新知架起“认知桥梁”，顺利地实现从旧知到新知的同化或顺应例如，学习“乘数是两位数的乘法”的认知基础是“乘数是一位数的乘法”。

课堂上，可先复习乘数是一位数的乘法，并向学生提出问题：“乘数是一位的乘法，用乘数去乘被乘数，所得积的末位应当写在哪一位上？为什么？”这一个问题促使学生真正弄懂所得的积是表示多少个1，应该把末位定在个位上的道理，从而很自然地认识到乘数是两位数时，用乘数十位上的数去乘被乘数，所得的积是表示多少个十，这时末位应该定位在十位的道理。

二.问重点重点，即重要的知识点，是由教材内容而定的，在整个知识结构中起纽带作用的知识点，是一堂课要解决的主要矛盾教师要针对重点，设计出关键性的问题，让学生集中精力去探索这一矛盾焦点，达到“达一发而动全身”的目的。

例如，教学“除数是小数的除法”时，教学的重点是除数小数点的处理教师必须先让学生练习除数是整数的除法（如3.2214），然后自然过渡到除数是小数的除法（如3.220.14），提出问题：这道题与上道题有什么不同？怎样使除数是小数的除法变成除数是整数的除法，而商的大小不变呢？这样，问题问在点子上，问在关键处，可以促使学生集中思维去探究除数的小数点处理。

三.问难点难点，即难学的知识点，是学生认知水平与抽象复杂的知识间的矛盾教师首先要充分估计学生思维活动中的种种障碍，准确地确定维难点难在何处，难点形成的原因，设计出化难为易的问题，促使学生层层深入、步步为营地攻克难点，真正子子子发挥难点对于发展学生思维能力的积极作用。

例如，在教学“多位数读写”时，中间有0的数的读写是教学中的一大难点根据例题：写出“五万零五”这个数，可设计下列问题：这个数的最高位在哪位上？这个数是几位数？这个数可分为哪几段？中间读出的一个零应该写几个0？。

四.问疑点疑点，即学生认知的疑惑点，一般表现在容易混淆和不易分清的知识点上教师要及时提出有利于解疑除惑的问题，使学生疑之成理、信之有据地明辩是非，提高思维的严谨性和准确性例如，在教学除数是纯小数的除法之前，学生接触到的除法运算中的商都比被除数小，于是，学生几乎都认为这是定律了。

当学到除数是纯小数的除法时，学生对商比被除数还大产生疑惑，教师可结合典型实例提出对比性的问题，来帮助学生弄通算理如，“有12个馒头，每人吃2个，能分给几个人吃呢？每人吃1个呢？每人吃半个呢？”教师将学生的算式板书出来，引导学生比较各式，学生便会茅塞顿开：“对呀，如果一个人吃半个，吃的人数当然比馒头的总数要多。

”进而领悟到“当除数大于1时，商就比被除数小；当除数等于1时，商和被除数同样大；当除数小于1时，商比被除数大”的规律了五.问盲点盲点，即弱信息的知识点，是指学生正常思维中容易被强信息干扰或掩盖的弱信息成分，即通常所说“容易被学生忽视的问题”。

教师要针对这些弱成分，设计出诱错问题，暴露学生的认知失误或思维偏差，再引导学生探究原因，达到“吃一堑，长一智”目的例如，判断一个分数能否化成有限小数时，学生往往忽视“一个最简分数”这一大前提针对这一情况，可提出问题：“。

能否化成有限小数？为什么？”围绕这个问题引导学生讨论，能促使学生深刻掌握运用这个判断方法时应注意的前提条件因才施问一.根据学生的情感倾向施问燕国材教授对情感在心理活动中的作用，打了一个绝妙的比喻：“情感是心理之‘车’的发动机，离开了情感这个发动机，学生的心理之‘车’就不会驰骋。

”然而，小学生的情感有明显的倾向性，他们对新奇的问题特别感兴趣，容易被不寻常的现象和内容所吸引为此，教师必须“投其所好”，创设新颖有趣的问题，激发学生有意义学习的心向例如，在教学“圆的认识”这节课时，一开始就向学生提出：“你们见过的车轮是什么形状的？”“有正方形、三角形的车轮吗？为什么？”“那么楕圆形的行不行？”随着这几个新奇问题和思考与讨论，学生处于积极思维状态，思维逐步逼近圆的本质特征。

教师再因势利导，必然收到顺水推舟之功效二.根据学生的认知水平施问课堂提问要触及学生的“最近发展区”，才能真正把学生推到主体地位上参与学习如果问题太简单，就不能启迪学生思维；如果问题太难，超越学生的认知水平，学生望而生畏，那就会挫伤学生的学习积极性。

这就需要教师深入了解学生的认知基础和思维水平，根据学生的认知水平量力而行，达到“让学生跳一跳，摘果子”的目的例如，教学“分数的基本性质”后，提问：“给9分之2的分子加上4后，要使分数大小不变，分母应加上什么数？”显然这个问题的难度与坡度都超越了学生的认知水平。

如果改为如下两个问题：9分之2的分子加上4，分子扩大了几倍？要使分数大小不变，分母应该怎么办？学生的思路就畅通了，比较适当三.根据学生的学习心态施问学生的学习心态直接影响着课堂教学的效果，特别是在学生情绪低落、注意力分散时，教师如果能审时度势，发挥教学机制，提出一些引人入胜、发人深省的问题，就能重新激起学生的学习热情，精神抖擞地投入学习活动。

例如，在教学“真分数与假分数”时，课临结束，学生认为自己已经掌握了真假分数的意义，思想开始松懈了这时教师提出问题：“b分之a是真分数，还是假分数？”学生中掀起思维高潮，在经过一番紧张的思考后，有人说：“是真分数”，也有人说：“是假分数”；还有人说：“可能是真分数，也可能是假分数。

”教师请大家说明理由，最后形成共识：当a四.根据学生的信息反馈施问课堂教学是师生双方信息交流的过程教师要敏锐洞悉学生的思维活动，准确及时地掌握学生反映出来的情况，迅速恰当地提出问题进行纠正补偿，使学生准确理解新知、完善认知结构。

例如，在教学运用商不变性质进行简便计算时，对8500200，学生列式如下：

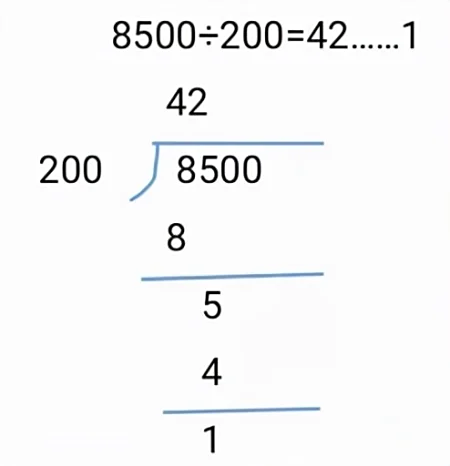
教师当机立断地提出下列问题：利用商不变性质，原式简化成什么式子计算？（852）在这里“85”表示什么？“2”又表示什么？（85个百，2个百）那么上面竖式中的余数“1”又表示什么呢？（1个百）学生就能很快地找出错误，并深刻认识到：被除数和除数同时缩小多少倍，所得的余数必须扩大相同的倍数，才是实际余数。

五.根据学生的个别差异施问学生之前的个别差异是客观存在的，数学教学不是为了消灭学生之间的个别差异，而应是实现有差异的发展为此，课堂提问不能搞“一刀切”，应有针对性地对不同的学生提出不同深度的问题，让不同层次的学生拥有同等的机会和成功感，达到全面发展的目的。

例如，讲完了“整除”和“除尽”后，教师出示算式：：204=5152=7.5120.5=24先叫后进生回答：“上面各式哪些是整除？哪些是除尽？”结果很可能是：“第式是整除，第式是除尽”再叫中等生补充，就可能会完整地说出：“第式是既整除，也是除尽，其它两个是除尽，而不是整除。

”最后叫优等生用整除和除尽的概念加以说明这样就能兼顾好、中、差三类学生，使各层次的学生各有所得和提高课堂提问“看似寻常最奇崛”问题既要针对教材内容，问在点子上，问在要害处；又要针对学生实际，提得启其心扉，促其思维。

这就需要教师刻苦钻研教材，深入了解学生，不断积累教学经验编辑：王改平审核：邢有军