高士达铝单板厂家电话多少（奇妙的数学知识）奇趣的数学，

天气越来越热，决定跟知友讲讲数学冷知识，来缓解一下。。。

1、 0! = 12、 x³=1，x有3个解3、

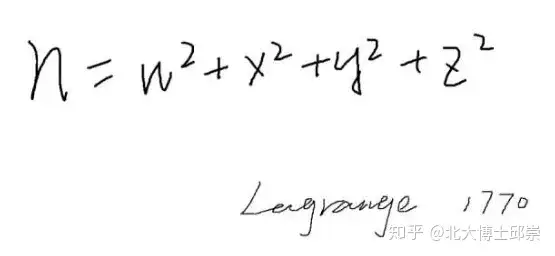
4、

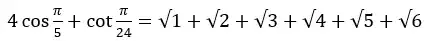
5、 任何一个带循环节的小数可以转化为分数。

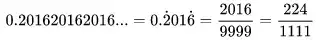
6、 1-1+1-1+1-1+1-…=1/21-2+3-4+5-6+7-…=1/41+2+3+4+5+6+7+.......=-1/127、 在轮盘赌中，盘上所有数字相加等于666。

8、 将一个硬币往上抛，得到字或者图向上的概率并不是0.5，图的概率会比字的要大因为字的那面比较重，所以呀，如果要猜，我们猜图的那面赢的概率会稍微大一点，尽管可以忽略不计……然后这个0.5只是传统概率学派所认为的，在贝叶斯学派里，他们认为这个概率应该是1。

9、 任意给定一个火腿三明治，总有一刀能把它切开，使得火腿、奶酪和面包片恰好都被分成两等份10、 如果一个房间里有23个或者23个以上的人，那么，有两个人生日是同一天的概率大于50%；如果人数超过50个，那么有两个人生日是同一天的概率将超过99%。

11、 喝醉的酒鬼总能找到回家的路，喝醉的小鸟则可能永远也回不了家。1921年，著名数学家波利亚（George Pólya）证明了这个定理。

假设有一条水平直线，从某个位置出发，每次有 50% 的概率向左走1米，有50%的概率向右走1米按照这种方式无限地随机游走下去，最终能回到出发点的概率是多少？答案是100% 在一维随机游走过程中，只要时间足够长，我们最终总能回到出发点。

现在考虑一个喝醉的酒鬼，他在街道上随机游走假设整个城市的街道呈网格状分布，酒鬼每走到一个十字路口，都会概率均等地选择一条路（包括自己来时的那条路）继续走下去那么他最终能够回到出发点的概率是多少呢？答案也还是 100% 。

刚开始，这个醉鬼可能会越走越远，但最后他总能找到回家路不过，醉酒的小鸟就没有这么幸运了假如一只小鸟飞行时，每次都从上、下、左、右、前、后中概率均等地选择一个方向，那么它很有可能永远也回不到 出发点了事实上，在三维网格中随机游走，最终能回到出发点的概率只有大约 34% 。

随着维度的增加，回到出发点的概率将变得越来越低在四维网格中随机游走，最终能回到出发点的概率是 19.3% ，而在八维空间中，这个概率只有 7.3% 12、 越是高维的球体，有越多的体积集中在靠近它的壳地方。

越是高维的球体，有越多的体积集中在靠近它的赤道面的地方而对于无穷维球体，有100%的体积集中在它的壳上，同时也有100%的体积集中在它的赤道面上又因为球是对称的， 所以，它的每个赤道面都集中了100%的体积，同时壳上也有100%的体积。

不过，无穷维球体体积是0，考虑到这一点的话，以上2个互相矛盾的性质就变得没那么不可思议了13、 三维空间的左手砍下来不能接在右手上，因为这样你的大拇指就朝向外侧了，然而，在四维空间里，这是可行的14、 自由意志定理：如果人有自由意志，那么基本粒子也有自由意志。

15、 分球定理：一个半径为1的实心球，可以剖分成有限的若干块，用这些块可以完整地重新拼出两个半径为1的实心球体！

简单来说就是，这样凭空产生了一个球16、 奇数与整数一样多，整数与有理数一样多，无理数比有理数多得多17、 身边的好妹子有那么多，你随手就能列举一大把，就像有理数一样可是在实数轴上随便戳一下，取（娶）到一个有理数（妹子）的概率是0。

18、 不可能事件概率一定是0%，而概率是0%的事件，有可能是可能事件19、 所有集合的集合不是一个集合20、 加法中的0等价于乘法中的1（即单位元）但是乘法中的0对应的却是加法中的无穷21、 一张厚0.1毫米的纸对折51次的厚度相当于绕赤道56189.3圈，比地球和太阳之间的距离还远。

22、 任何数学方法都无法指出 i 和 -i 到底区别在哪里23、 本福特法则：在一堆从实际生活得出的数据中，以1为首位数字的数的出现概率约为总数的三成，是人们通常期望值 1/9 的 3 倍越大的数，以它为首几位的数出现的机率就越低。

它可用于检查各种数据是否有造假24、 不动点定理：把一张世界地图揉成一团丢地上，地图上的一个点必定和现实中这个点相重合25、 离散数学：如果命题p为假，则无论命题q是真还是假，p→q（若p则q）始终是真的。

来举三个例子：“若1+1=2，则我是邱崇。”是真命题；“若1+1=1，则我是邱崇。”是真命题；“若1+1=1，则我是一只猪。”也是真命题。